Das Potenzieren hat im Gegensatz zu den Grundrechenarten Addieren und Multiplizieren zwei Umkehrrechenarten.
Der Gund dafür ist, dass die beiden „Partner“ Basis ![]() und Exponent
und Exponent ![]() bei einer Potenz
bei einer Potenz ![]() unterschiedliche Bedeutungen haben.
unterschiedliche Bedeutungen haben.
Um die Basis ![]() bei gegebenen Werten für Exponent
bei gegebenen Werten für Exponent ![]() und Potenzwert
und Potenzwert ![]() zu bestimmen, musst du Radizieren, also die Wurzel ziehen. Ein Beispiel: Aus
zu bestimmen, musst du Radizieren, also die Wurzel ziehen. Ein Beispiel: Aus ![]() erhältst du die Basis mit
erhältst du die Basis mit ![]() , also ist
, also ist ![]() .
.
Um den Exponenten ![]() bei gegebenen Werten für Basis
bei gegebenen Werten für Basis ![]() und Potenzwert
und Potenzwert ![]() zu bestimmen, musst du Logarithmieren. Beispiel: Aus
zu bestimmen, musst du Logarithmieren. Beispiel: Aus ![]() erhältst du
erhältst du ![]() mit
mit ![]() , denn
, denn ![]() .
.
Definition: Der Logarithmus einer positiven reellen Zahl
zur Basis
ist der Exponent, mit dem man die Basis potenzieren muss, um die gegebene Zahl zu erhalten.
Ist also ![]() , so gilt also
, so gilt also ![]() .
.
Beispiele
 , denn
, denn 
 , denn
, denn 
 , denn
, denn 
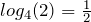 , denn
, denn 
 , denn
, denn 
 , denn
, denn 
 , denn
, denn 
Logarithmensysteme
Logarithmen können als Basis beliebige positive reelle Zahlen ![]() haben. Einige Basen werden jedoch häufig verwendet.
haben. Einige Basen werden jedoch häufig verwendet.
Der Logarithmus zur Basis ![]() heißt dekadischer Logarithmus oder Zehnerlogarithmus. Er wird meistens mit
heißt dekadischer Logarithmus oder Zehnerlogarithmus. Er wird meistens mit ![]() abgekürzt (auf Taschenrechnern kann jedoch auch
abgekürzt (auf Taschenrechnern kann jedoch auch ![]() auf der Taste stehen wie zum Beispiel beim Casio):
auf der Taste stehen wie zum Beispiel beim Casio): ![]()
Der Logarithmus zur Basis ![]() heißt natürlicher Logarithmus und wird mit
heißt natürlicher Logarithmus und wird mit ![]() (von logarithmus naturalis) abgekürzt:
(von logarithmus naturalis) abgekürzt: ![]()
In der Informatik spielt manchmal auch der Logarithmus zur Basis ![]() eine Rolle; er heißt binärer Logarithmus oder Zweierlogarithmus und wird geschrieben als
eine Rolle; er heißt binärer Logarithmus oder Zweierlogarithmus und wird geschrieben als ![]() .
.
Rechengesetze für Logarithmen
Da Logarithmieren eine Umkehrung des Potenzierens ist, folgen aus Regeln für das Potenzieren bei gleicher Basis entsprechende Regeln für die Logarithmen.
| Potenzgesetz | Logarithmengesetz |
| |
Da Potenzieren und Logarithmieren Umkehroperationen voneinander sind, heben sie sich gegenseitig auf. Es gilt also zum Beispiel für den natürlichen Logarithmus: ![]() und
und ![]() .
.
Umwandlung von Logarithmensystemen
Viele Taschenrechner kennen nur den dekadischen und den natürlichen Logarithmus, dann ist es notwendig, einen beliebigen Logarithmus mit Hilfe zum Beispiel des natürlichen Logarithmus zu berechnen. Wegen ![]() gilt
gilt ![]() und deshalb:
und deshalb:
![]()
Statt des natürlichen Logarithmus kann man genauso gut den Zehnerlogarihmus benutzen. Der Casio kann auch einen Logarithmus zu einer beliebigen Basis berechnen.
Verwendung von Logarithmen
In der Vortaschenrechnerzeit waren die Logarithmen sehr wichtig, weil man mit ihrer Hilfe leichter multiplizieren, dividieren, potenzieren oder radizieren konnte. In alten Formelsammlungen gibt es lange Tabellen mit Logarithmen, und auch Rechenschieber arbeiten mit dem Konzept der Logarithmen.
Heutzutage sind Logarithmen noch wichtig bei der Beschreibung von sehr stark wachsenden Zahlenreihen wie etwa der Schalldruck, der in Dezibel angegeben wird, oder der Richterskala oder dem ph-Wert …
In der Schule brauchen wir die Logarithmen meistens zum Lösen von Exponentialgleichungen. Der natürliche Logarithmus ist weiterhin eine Stammfunktion der Funktion ![]() (der Reziprokfunktion).
(der Reziprokfunktion).
Beispiele für das Lösen von Exponentialgleichungen
Beispiel 1:
Eine Bakterienkultur mit 300 Bakterien vermehrt sich in einer Nährlösung stündlich um ![]() . Nach welcher Zeit hat sich die Bakterienzahl verdoppelt?
. Nach welcher Zeit hat sich die Bakterienzahl verdoppelt?
Für die Wachstumsfunktion ![]() gilt:
gilt:
![]()
Gesucht ist die Zeit ![]() , für die
, für die ![]() ist. Daher gilt die Gleichung:
ist. Daher gilt die Gleichung:
![]()
oder
![]()
Die gesuchte Zeit ist dann
![]()
Die Bakterien haben sich also nach 9 Stunden verdoppelt. Die anfängliche Bakterienzahl spielt übrigens keine Rolle (warum?).
Beispiel 2:
Für Radon 220 gilt die Zerfallsfunktion ![]() . Wie groß ist die Halbwertszeit, d.h. die Zeit, in der die Hälfte aller Atome zerfallen sind?
. Wie groß ist die Halbwertszeit, d.h. die Zeit, in der die Hälfte aller Atome zerfallen sind?
Gesucht ist die Zeit ![]() , für die
, für die ![]() ist. Daher gilt die Gleichung:
ist. Daher gilt die Gleichung:
![]()
oder
![]()
Dann ist
![]()
und
![]()
Es dauert 55 Sekunden, bis die Hälfte der Atome Radon 220 zerfallen sind.
