- Punkte und Vektoren
- Vektoren
- Lineare Abhängigkeit
- Die Vektorsumme
- Linearkombination
Definition:
Vektoren 
heißen linear unabhängig, falls sich kein Vektor von ihnen als Linearkombination der übrigen Vektoren darstellen lässt.
Kann man wenigstens einen der Vektoren als Linearkombination der übrigen Vektoren darstellen, so heißen die Vektoren linear abhängig.
Zwei Vektoren
- Zwei Vektoren
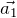und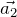 
sind linear unabhängig, wenn sie nicht parallel sind. - Wenn zwei Vektoren linear abhängig sind, sagt man auch, sie sind kollinear.
Drei Vektoren
- In einer zweidimensionalen Ebene sind drei Vektoren immer linear abhängig.
- Wenn sich dreidimensionalen Raum ein Vektor als Linearkombination schreiben lässt, liegen die drei Vektoren in einer Ebene; man sagt die Vektoren sind komplanar.
- Liegen die Vektoren nicht in einer Ebene, sind sie linear unabhängig.
Vier Vektoren
- Vier Vektoren sind immer linear abhängig (zumindest in unserer dreidimensionalen Welt).
In zwei Dimensionen
In der Grafik sind links alle Vektoren paarweise linear abhängig. Gib die Vektoren 
, 
und 
als Vielfache des Vektors 
an. Gib den Vektor 
als Vielfaches des Vektors
an. Tipp: Die Vektoren lassen sich bewegen.
Dr. Marie-Luise Herrmann, erstellt mit GeoGebra
Die beiden Vektoren und 
rechts sind linear unabhängig.
In drei Dimensionen
Die beiden folgenden Grafiken sehen fast gleich aus. Betrachte sie jeweils aus anderen Sichtpunkten, indem du sie drehst. Du kannst auch die (roten) Punkte verändern.
In welcher Grafik werden linear abhängige (komplanare), in welcher linear unabhängige Vektoren dargestellt?
Dr. Marie-Luise Herrmann, erstellt mit GeoGebra