Series: GeoGebra-Kurs

Ein kleiner GeoGebra-Kurs zum Kennenlernen.

Gleichungen

Dieser Beitrag ist Teil 12 von 18 in der Reihe GeoGebra-Kurs
 

Die wichtigste Eigenschaft das CAS-Moduls von GeoGebra ist meiner Meinung nach, dass es Gleichungen lösen kann. Manche Gleichungen lassen sich auch im Algebra-Fenster lösen, wenn es zum Beispiel um Nullstellen oder Schnittstellen geht. Das CAS-Modul löst Gleichungen aber auch symbolisch, wenn die Gleichungen Parameter enthält.

„Gleichungen“ weiterlesen

Gleichungen lösen

Dieser Beitrag ist Teil 13 von 18 in der Reihe GeoGebra-Kurs
 

Der einfachste Befehl zum Lösen von Gleichungen heißt in GeoGebra
Löse[ <Gleichung in x> ]. Die zugehörige Beschreibung ist:
Löst die angegebene Gleichung für die Variable x und erzeugt eine Liste mit allen Lösungen. Dieser Befehl entspricht in etwa dem Löse-Werkzeug  (siehe Aufgabe 3 aus CAS-Fenster).

„Gleichungen lösen“ weiterlesen

Lineare Gleichungssysteme

Dieser Beitrag ist Teil 14 von 18 in der Reihe GeoGebra-Kurs
 

LGS mit zwei Unbekannten

Eine lineare Gleichung mit zwei Variablen kann auf die Form a \cdot x + b \cdot y = c gebracht werden (dabei dürfen nicht beide Variablen a und b den Wert 0 haben). Eine solche Gleichung entspricht grafisch einer Geraden; jeder Punkt dieser Geraden bildet ein Lösungspaar (x, y) der Gleichung. Es gibt also unendlich viele Lösungen.

„Lineare Gleichungssysteme“ weiterlesen

LGS lösen mit Löse

Dieser Beitrag ist Teil 15 von 18 in der Reihe GeoGebra-Kurs
 

Mit dem CAS-Befehl Löse lassen sich auch Gleichungssysteme lösen. Dann wird aber die Syntax Löse[<Liste von Gleichungen>,<Liste von Variablen>] verwendet. Eine Liste erhältst du, indem du mehrere Objekte (Punkte, Strecken, Funktionen, Gleichungen, …) mit geschweiften Klammern zusammenfasst. In Zeile 4 habe ich die Gleichungen gl1, gl2, gl3 zu einer Liste zusammengefasst und direkt in den Befehl Löse eingetragen. In Zeile 5 habe ich der Liste mit den Gleichungen gl1, gl2, gl3 den Namen lgs gegeben. In Zeile 6 habe ich nur diesen Namen verwendet. Da in den drei Gleichungen nur drei Variablen vorkommen, kann man in diesem Fall sogar die Liste von Variablen weglassen.

„LGS lösen mit Löse“ weiterlesen

LGS lösen mit einer Matrix

Dieser Beitrag ist Teil 16 von 18 in der Reihe GeoGebra-Kurs
 

Auf der Seite Lineare Gleichungssysteme haben wir als Beispiel das LGS

    \begin{align*}3x+6y-2z&=-15\\3x+2y+z&=2\\2x+5y-5z&=-23\end{align*}

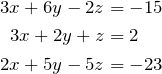
kennengelernt. Diesem LGS entspricht die erweiterte Koeffizientenmatrix:

\begin{pmatrix}3&6&-2&-15\\3&2&1&2\\2&5&-5&-23\end{pmatrix}

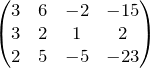
Bei einer Koeffizienzenmatrix lassen sich die gleichen Zeilenumformungen durchführen wie bei einem normalen LGS. So könnte man dann die Matrix

\begin{pmatrix}3&6&-2&-15\\0&-4&3&17\\0&0&-35&-105\end{pmatrix}

erhalten, die der Stufenform entspricht. Wenn man noch weitere Zeilenumformungen vornimmt, kann man zu der Form

\begin{pmatrix}1&0&0&1\\0&1&0&-2\\0&0&1&3\end{pmatrix}

gelangen. Diese Form heißt auch die reduzierte Stufenform oder Treppennormalform. GeoGebra kennt diese auch:

Aus der Treppennormalform lassen sich die Lösungen unmittelbar ablesen: x = 1, y = -2 und z = 3. Genial einfach!

Online-Version von GeoGebra