Wenn von einer Größe die lokale (bzw. momentane) Änderungsrate in einem Intervall bekannt ist, lässt sich daraus auf die gesamte Veränderung der Größe schließen, also die Wirkung der lokalen Änderungsrate bestimmen. Wenn man zum Beispiel die Geschwindigkeit eines Fahrzeugs kennt, kann man daraus den zurückgelegten Weg ermitteln. Ist die Geschwindigkeit 
konstant, ist der zurückgelegte Weg einfach 
. Etwas komplizierter wird es, wenn die Geschwindigkeit nicht konstant ist.
Aufgabe
In der folgenden Grafik wird ein Bremsvorgang dargestellt. Ein PKW fährt mit einer Geschwindigkeit von 
, als der Fahrer einen Messpunkt passiert. 10 Sekunden später bremst er, und kommt nach weiteren 10 Sekunden zum Stillstand.
- Berechne den Weg, den der PKW in den ersten 2, 4, 10 Sekunden nach Passieren des Messpunktes zurücklegt.
- Wie kannst du die Ergebnisse geometrisch interpretieren?
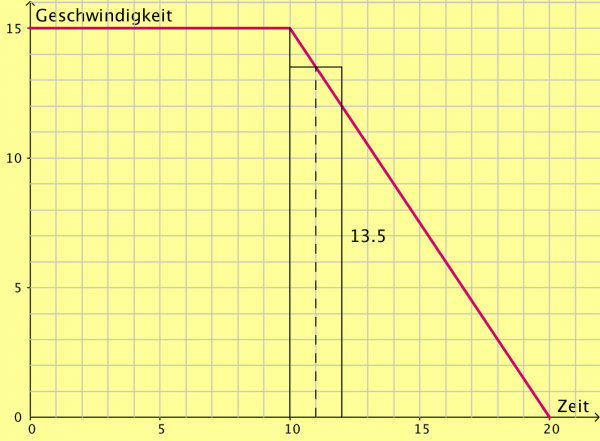
- Berechne den Weg, den der PKW zwischen der 10. und 12. Sekunde zurücklegt. Tipp: Rechne mit der Durchschnittgeschwindigkeit in dem Zeitintervall.
- Berechne auch für die nächsten 2 Sekunden langen Zeitintervalle die zurückgelegten Wege.
- Wie kannst du diese Ergebnisse geometrisch interpretieren?
- Stelle alles in einer Tabelle dar und bestimme auch die Gesamtwege für die Zeit nach Passieren des Messpunktes.
- Trage die Gesamtwege in ein Koordinatensystem ein.
Das Ergebnis sieht dann etwa wie folgt aus:
In der Tabelle steht in der Spalte B die mittlere Geschwindigkeit in den Zeitintervallen. Der Graph zeigt den Gesamtweg als Funktion der Zeit an, sozusagen die Wirkungsfunktion des Geschwindigkeit.
Die Wege in den Zeitintervallen lassen sich geometrisch als Inhalt der Fläche zwischen der Geschwindigkeit und der x-Achse deuten. Der Gesamtweg entspricht der gesamten Fläche unter dem Geschwindigkeitsgraphen zwischen 
und 
.
Mit solchen Problemen beschäftigt sich die Integralrechnung.